El Teorema del Límite Central es uno de los conceptos fundamentales en la teoría de la probabilidad y la estadística. Este teorema establece que, bajo ciertas condiciones, la suma de un gran número de variables aleatorias independientes y con la misma distribución tiende a seguir una distribución normal. En otras palabras, este teorema nos permite comprender cómo se comporta la media de una muestra cuando el tamaño de la muestra es grande.
Este teorema es de gran importancia en la estadística, ya que nos permite realizar inferencias sobre una población a partir de una muestra. Además, es utilizado en diversos campos como la econometría, la biología, la física y la ingeniería, entre otros. Comprender este teorema nos ayuda a entender cómo se distribuyen los datos y cómo podemos utilizar esta información para tomar decisiones informadas.
Teorema de Bernoulli
El teorema de Bernoulli es un concepto fundamental en la teoría de la probabilidad y estadística. Fue formulado por el matemático suizo Jacob Bernoulli en el siglo XVIII y establece una relación entre la probabilidad de un evento y el número de veces que se repite dicho evento.
En términos simples, el teorema de Bernoulli establece que a medida que el número de repeticiones de un experimento aumenta, la probabilidad de que ocurra un evento específico se acerca a un valor constante. Esto significa que, en condiciones ideales, la probabilidad de un evento se estabiliza a medida que se realizan más repeticiones del experimento.
Este teorema es especialmente útil en situaciones en las que se realizan múltiples experimentos independientes, como lanzar una moneda o tirar un dado. Permite predecir la probabilidad de obtener un resultado específico en función del número de repeticiones del experimento.
En resumen, el teorema de Bernoulli es una herramienta fundamental en la teoría de la probabilidad y estadística que establece una relación entre la probabilidad de un evento y el número de veces que se repite dicho evento. Su comprensión es esencial para entender conceptos más avanzados, como el teorema del límite central.
Definición del Teorema del Límite Central
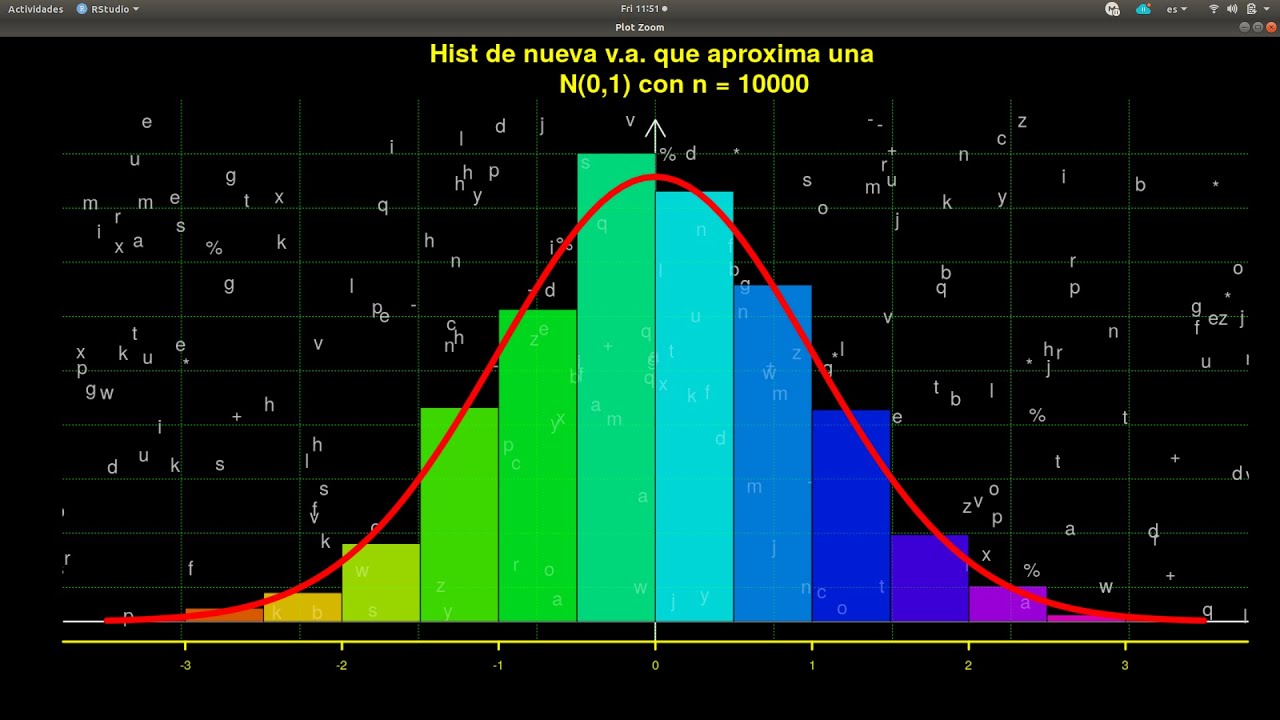El Teorema del Límite Central es uno de los conceptos fundamentales en la teoría de la probabilidad y la estadística. Este teorema establece que, bajo ciertas condiciones, la suma de un gran número de variables aleatorias independientes y con la misma distribución tiende a seguir una distribución normal.
En otras palabras, el Teorema del Límite Central nos dice que, sin importar la forma de la distribución original de las variables aleatorias, cuando se suman en grandes cantidades, su distribución se aproxima a una distribución normal. Esto es de gran importancia, ya que la distribución normal es ampliamente utilizada en la estadística y permite realizar inferencias y estimaciones precisas sobre una población.
Aplicaciones del Teorema del Límite Central
El Teorema del Límite Central es uno de los conceptos fundamentales en la teoría de la probabilidad y la estadística. Este teorema establece que, bajo ciertas condiciones, la suma de un gran número de variables aleatorias independientes y con la misma distribución tiende a seguir una distribución normal. Esto tiene importantes aplicaciones en diversos campos.
Una de las aplicaciones más comunes del Teorema del Límite Central es en la inferencia estadística. Cuando se realiza un estudio o experimento, es común que se obtengan muestras de una población para realizar estimaciones o tomar decisiones. El Teorema del Límite Central permite utilizar la distribución normal para hacer inferencias sobre la población a partir de las muestras, lo que facilita el análisis de datos y la toma de decisiones.
Otra aplicación del Teorema del Límite Central es en la modelización de fenómenos naturales o sociales. Muchos fenómenos en la naturaleza y en la sociedad pueden ser modelados como la suma de múltiples variables aleatorias. El Teorema del Límite Central permite aproximar la distribución de estos fenómenos a una distribución normal, lo que facilita su estudio y comprensión.
Importancia del Teorema del Límite Central en la estadística
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y tiene una gran importancia en el análisis de datos. Este teorema establece que, cuando se toman muestras aleatorias de cualquier distribución, la distribución de las medias de esas muestras se aproxima a una distribución normal a medida que el tamaño de la muestra aumenta.
Esta propiedad es de vital importancia en la inferencia estadística, ya que nos permite hacer suposiciones sobre la población a partir de una muestra. Al tener una distribución normal, podemos utilizar técnicas estadísticas que se basan en esta distribución, como la construcción de intervalos de confianza y la realización de pruebas de hipótesis.
Además, el Teorema del Límite Central nos permite entender mejor el comportamiento de las muestras y cómo se relacionan con la población. Nos ayuda a comprender que, incluso si la población no sigue una distribución normal, las medias de las muestras sí lo hacen, lo que nos brinda una herramienta poderosa para el análisis estadístico.
Relación entre el Teorema del Límite Central y la distribución normal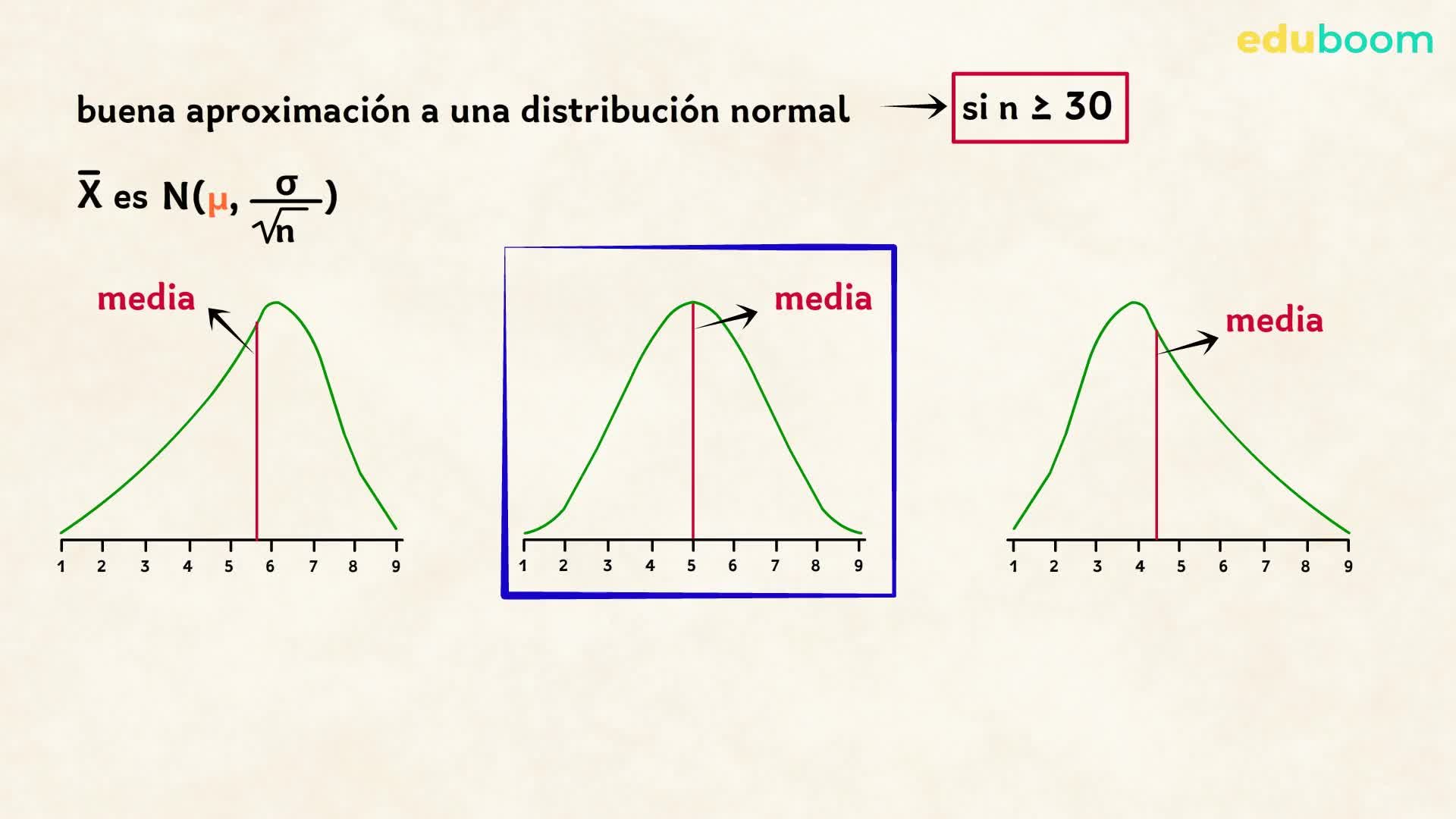
El Teorema del Límite Central (TLC) es uno de los conceptos fundamentales en estadística y tiene una estrecha relación con la distribución normal. El TLC establece que, cuando se toman muestras aleatorias de cualquier población, la distribución de las medias muestrales se aproxima a una distribución normal a medida que el tamaño de la muestra aumenta.
En otras palabras, el TLC nos dice que, sin importar la forma de la distribución original de la población, si tomamos suficientes muestras de tamaño n y calculamos la media de cada una de ellas, la distribución de estas medias se acercará a una distribución normal. Esto es especialmente útil cuando no conocemos la distribución de la población y queremos hacer inferencias sobre ella.
La distribución normal, también conocida como la campana de Gauss, es una de las distribuciones más importantes en estadística. Tiene propiedades bien definidas y es ampliamente utilizada en la modelización de fenómenos naturales y sociales. El TLC nos permite utilizar la distribución normal como una aproximación para la distribución de las medias muestrales, lo que simplifica los cálculos y nos permite hacer inferencias más precisas.
En resumen, el Teorema del Límite Central establece que la distribución de las medias muestrales se aproxima a una distribución normal a medida que el tamaño de la muestra aumenta. Esto nos permite utilizar la distribución normal como una aproximación para hacer inferencias sobre la población, incluso cuando no conocemos la forma de su distribución original.
Limitaciones del Teorema del Límite Central
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y probabilidad. Este teorema establece que, bajo ciertas condiciones, la distribución de la media de una muestra tiende a aproximarse a una distribución normal a medida que el tamaño de la muestra aumenta. Sin embargo, es importante tener en cuenta que el Teorema del Límite Central tiene algunas limitaciones.
Una de las limitaciones más importantes del Teorema del Límite Central es que solo se aplica a muestras grandes. Esto significa que, para que el teorema sea válido, el tamaño de la muestra debe ser lo suficientemente grande. Si el tamaño de la muestra es pequeño, el Teorema del Límite Central puede no ser aplicable y la distribución de la media de la muestra puede no aproximarse a una distribución normal.
Otra limitación del Teorema del Límite Central es que solo se aplica a variables aleatorias independientes e idénticamente distribuidas. Esto significa que las observaciones en la muestra deben ser independientes entre sí y seguir la misma distribución. Si las observaciones no son independientes o no siguen la misma distribución, el Teorema del Límite Central no se puede aplicar y la distribución de la media de la muestra puede no ser normal.
Teorema del Límite Central y el muestreo aleatorio
El Teorema del Límite Central es uno de los conceptos fundamentales en la estadística y tiene una gran importancia en la comprensión de cómo funciona el muestreo aleatorio. Este teorema establece que, cuando se toman muestras aleatorias de cualquier población, la distribución de las medias de esas muestras se aproxima a una distribución normal, independientemente de la forma de la distribución original.
En otras palabras, el Teorema del Límite Central nos dice que, si tomamos muchas muestras aleatorias de una población y calculamos la media de cada una de esas muestras, obtendremos una distribución de medias que se asemeja a una distribución normal. Esto es cierto incluso si la población original no sigue una distribución normal.
Este concepto es de vital importancia en la estadística porque nos permite hacer inferencias sobre una población utilizando solo una muestra. Al tener una distribución de medias que se aproxima a una distribución normal, podemos utilizar las propiedades conocidas de la distribución normal para realizar estimaciones y pruebas de hipótesis.
Teorema del Límite Central y la inferencia estadística
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y juega un papel crucial en la inferencia estadística. Este teorema establece que, independientemente de la forma de la distribución original de una población, la distribución de la media de una muestra tiende a aproximarse a una distribución normal a medida que el tamaño de la muestra aumenta.
En otras palabras, el Teorema del Límite Central nos permite hacer inferencias sobre una población utilizando muestras, ya que nos asegura que la media de las muestras se distribuirá de manera normal. Esto es de gran importancia, ya que nos permite utilizar técnicas estadísticas basadas en la distribución normal, como la construcción de intervalos de confianza y la realización de pruebas de hipótesis.
Además, el Teorema del Límite Central nos proporciona una medida de la precisión de nuestras estimaciones. Cuanto mayor sea el tamaño de la muestra, más precisa será nuestra estimación de la media poblacional. Esto nos permite tener mayor confianza en los resultados obtenidos a partir de nuestras muestras y tomar decisiones informadas basadas en la inferencia estadística.
Teorema del Límite Central y la estimación de parámetros
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y tiene una gran importancia en la estimación de parámetros. Este teorema establece que, bajo ciertas condiciones, la distribución de la media muestral de una población se aproxima a una distribución normal a medida que el tamaño de la muestra aumenta.
En otras palabras, el Teorema del Límite Central nos dice que, sin importar la forma de la distribución original de la población, si tomamos muestras aleatorias de tamaño suficientemente grande, la distribución de las medias de esas muestras se aproximará a una distribución normal. Esto es de gran utilidad, ya que nos permite hacer inferencias sobre la población a partir de la muestra.
La importancia de este teorema radica en que nos permite estimar parámetros poblacionales, como la media o la proporción, a partir de la media muestral. Al tener una distribución normal, podemos utilizar técnicas estadísticas para calcular intervalos de confianza y realizar pruebas de hipótesis, lo que nos brinda información precisa sobre los parámetros de interés.
En resumen, el Teorema del Límite Central es esencial en la estimación de parámetros, ya que nos permite hacer inferencias sobre la población a partir de la muestra. Su importancia radica en que nos proporciona una base sólida para realizar análisis estadísticos y tomar decisiones basadas en datos.
Teorema del Límite Central y la prueba de hipótesis
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y juega un papel crucial en la prueba de hipótesis. Este teorema establece que, bajo ciertas condiciones, la distribución de la media de una muestra se aproxima a una distribución normal, sin importar la forma de la distribución original de los datos.
En otras palabras, el Teorema del Límite Central nos permite inferir información sobre una población a partir de una muestra, ya que nos dice que la media muestral se comporta de manera predecible. Esto es especialmente útil cuando queremos realizar pruebas de hipótesis, donde comparamos una muestra con una hipótesis nula y determinamos si hay evidencia suficiente para rechazarla o no.
La prueba de hipótesis es una herramienta estadística que nos permite tomar decisiones basadas en la evidencia de una muestra. Utilizando el Teorema del Límite Central, podemos calcular la probabilidad de obtener una muestra con una media igual o más extrema que la observada, asumiendo que la hipótesis nula es verdadera. Si esta probabilidad es lo suficientemente baja, podemos rechazar la hipótesis nula y concluir que hay evidencia para apoyar la hipótesis alternativa.
Teorema del Límite Central y la regresión lineal
El Teorema del Límite Central es uno de los conceptos fundamentales en estadística y tiene una gran importancia en la regresión lineal. Este teorema establece que, cuando se tienen muestras aleatorias de una población, la distribución de las medias de esas muestras se aproxima a una distribución normal a medida que el tamaño de las muestras aumenta.
En el contexto de la regresión lineal, el Teorema del Límite Central es relevante porque nos permite hacer inferencias sobre los coeficientes de la regresión. Al tener una muestra aleatoria de datos, podemos utilizar el teorema para obtener una distribución aproximada de los coeficientes y así realizar pruebas de hipótesis y construir intervalos de confianza.
Además, el Teorema del Límite Central nos permite entender la variabilidad de los estimadores de la regresión lineal. Al tener una distribución aproximada de los coeficientes, podemos evaluar la precisión de nuestras estimaciones y determinar qué tan confiables son.
Teorema del Límite Central y la econometría
El Teorema del Límite Central es uno de los conceptos fundamentales en la estadística y la econometría. Este teorema establece que, bajo ciertas condiciones, la distribución de la media de una muestra tiende a aproximarse a una distribución normal a medida que el tamaño de la muestra aumenta. En otras palabras, este teorema nos permite hacer inferencias sobre la población a partir de una muestra.
En el campo de la econometría, el Teorema del Límite Central es especialmente relevante. La econometría es una disciplina que combina la economía y la estadística para analizar y predecir fenómenos económicos. Al utilizar técnicas de muestreo y estimación, los econometristas pueden aplicar el Teorema del Límite Central para obtener conclusiones más precisas sobre las relaciones entre variables económicas.
Por ejemplo, supongamos que un econometrista desea estudiar el impacto de la inversión en educación en el crecimiento económico. Para ello, recopila datos de diferentes países y realiza un análisis de regresión. Al aplicar el Teorema del Límite Central, el econometrista puede obtener estimaciones más confiables de los coeficientes de la regresión y realizar inferencias sobre la relación entre la inversión en educación y el crecimiento económico a nivel de la población.
Aprende sobre el siguiente tema: Torricelli Teorema